1. 概要
統計学は、データを収集・分析・解釈するための方法論を提供する学問分野です。応用情報技術者試験のシラバスにおける「確率と統計」の「統計」の項目では、データの特性を把握し、そこから有用な情報を引き出すための基本的な統計手法について理解することが求められています。
現代社会においては、ビッグデータの活用やAI技術の発展により、統計学の重要性はますます高まっています。IT技術者として、適切なデータ分析手法を選択し、得られた結果を正しく解釈する能力は必須となっています。
2. 詳細説明
2.1. データの分布と代表値
2.1.1. 度数分布表とヒストグラム
度数分布表は、データをいくつかの階級に分け、各階級に含まれるデータの個数(度数)を表にまとめたものです。ヒストグラムは、度数分布表をグラフ化したもので、データの分布の形状を視覚的に把握するのに役立ちます。
図1: 度数分布表とヒストグラムの例
2.1.2. 代表値
代表値は、データ全体の特徴を表す値です。主な代表値には以下のようなものがあります:
- 平均値:全データの合計をデータ数で割った値
- 中央値(メジアン):データを大きさ順に並べたときに中央に位置する値
- 最頻値(モード):データの中で最も頻繁に現れる値
2.1.3. ばらつきの指標
データのばらつきを示す指標には以下のようなものがあります:
- 分散:各データの平均値からの偏差の二乗の平均
- 標準偏差:分散の正の平方根
- 歪度:分布の非対称性を表す指標
- 尖度:分布の裾の重さを表す指標
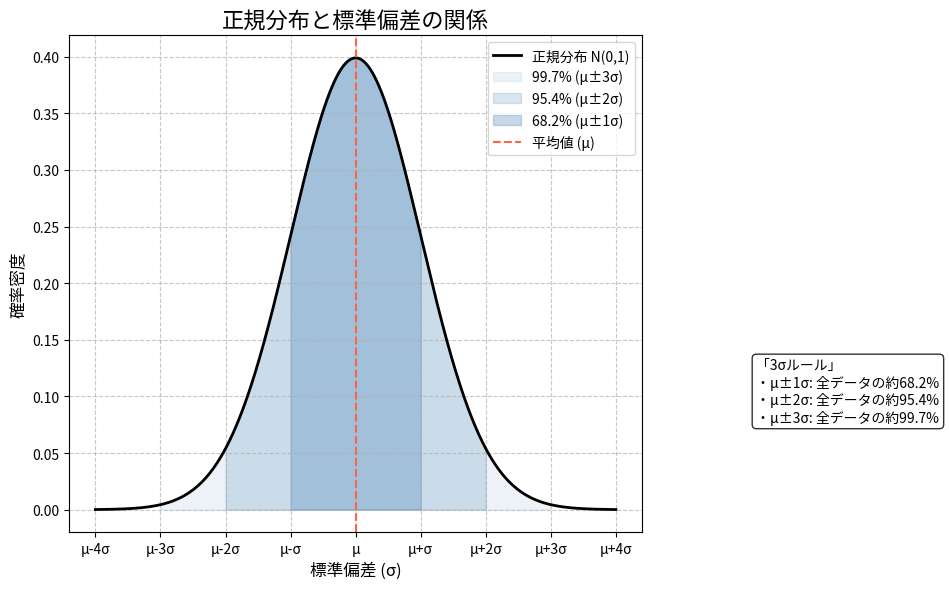
図2: 正規分布と標準偏差の関係
2.2. 相関と回帰
2.2.1. 相関分析
相関分析は、2つの変数間の関連性の強さを測定する手法です。相関係数は-1から1の間の値をとり、絶対値が大きいほど強い関連があることを示します。ただし、相関と因果は異なる概念であり、相関関係があるからといって因果関係があるとは限りません。また、第三の変数の影響による疑似相関にも注意が必要です。
図3: 相関係数と散布図の関係
2.2.2. 回帰分析
回帰分析は、説明変数と目的変数の関係をモデル化する手法です。
- 単回帰分析:1つの説明変数から目的変数を予測
- 重回帰分析:複数の説明変数から目的変数を予測
- ロジスティック回帰分析:目的変数が二値(0/1)の場合に用いる回帰分析
回帰分析を行う際には、回帰直線を求めることで、変数間の関係を数式として表現できます。
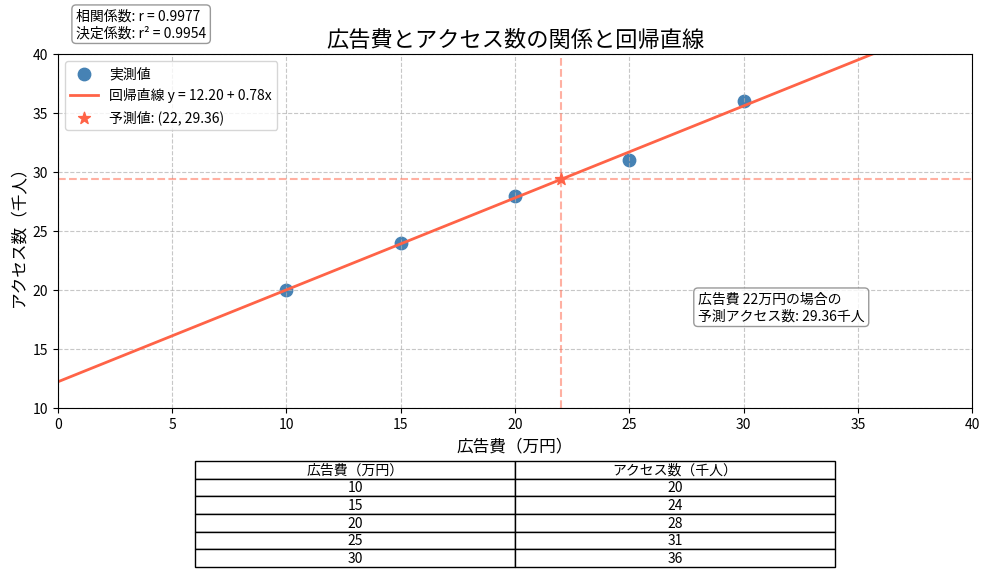
図4: 回帰直線の例
2.3. 多変量解析
多変量解析は、多数の変数を同時に分析する手法です。
- 主成分分析:多数の変数を少数の主成分に要約する手法
- 因子分析:観測された変数の背後にある潜在的な因子を探る手法
2.4. データの尺度
データの性質に応じて、以下の4つの尺度に分類されます:
- 名義尺度:分類のみを目的とした尺度(例:性別、血液型)
- 順序尺度:順序関係を持つ尺度(例:成績のA, B, C)
- 間隔尺度:等間隔性を持つが絶対的なゼロ点がない尺度(例:温度(℃))
- 比例尺度:等間隔性と絶対的なゼロ点を持つ尺度(例:身長、体重)
| 尺度 | 特徴 | 例 | 可能な統計処理 |
|---|---|---|---|
| 名義尺度 (Nominal Scale) |
|
|
|
| 順序尺度 (Ordinal Scale) |
|
|
|
| 間隔尺度 (Interval Scale) |
|
|
|
| 比例尺度 (Ratio Scale) |
|
|
|
表1: データの4つの尺度と例
2.5. 統計的推測
2.5.1. 推定
推定は、標本から母集団のパラメータを推測する手法です。
- 点推定:パラメータを単一の値で推定
- 区間推定:パラメータを一定の信頼区間で推定
推定には尤度の概念が重要で、最尤推定はデータが得られる確率が最大になるようなパラメータを選ぶ方法です。
2.5.2. 仮説検定
仮説検定は、統計的仮説の妥当性を検証する手法です。
- 帰無仮説:検定で否定したい仮説
- 対立仮説:帰無仮説が棄却された場合に採択される仮説
- 有意水準:帰無仮説を棄却するための基準となる確率
- p値(有意確率):観測されたデータまたはそれよりも極端なデータが、帰無仮説のもとで得られる確率
- 棄却域:帰無仮説を棄却する検定統計量の値の範囲
仮説検定には、以下のような誤りのリスクがあります:
- 第1種の誤り:実際は正しい帰無仮説を棄却してしまう誤り
- 第2種の誤り:実際は誤りの帰無仮説を棄却できない誤り
- 検出力(検定力):真の効果を検出できる確率(1-第2種の誤りの確率)
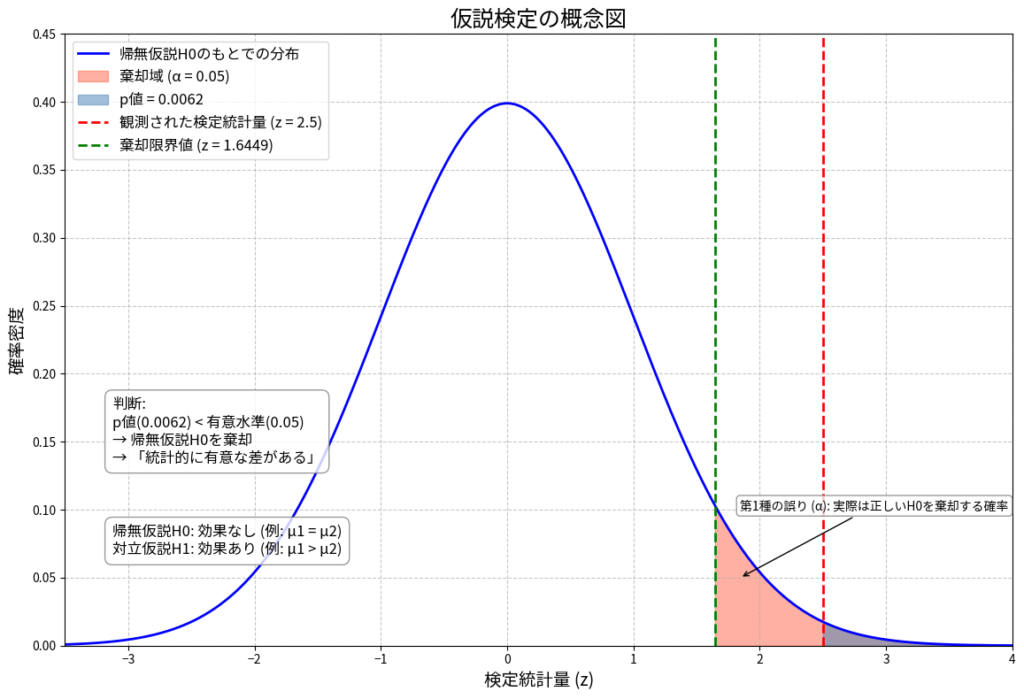
図5: 仮説検定の概念図
2.5.3. 主な検定手法
- t検定:平均値の差の検定によく使用
- z検定:大きなサンプルサイズでの平均値の検定
- カイ二乗検定:カテゴリカルデータの独立性や適合度の検定
- 分散分析:3つ以上のグループの平均値の差の検定
| 検定手法 | 用途 | 使用条件 | 特徴 | 利用例 |
|---|---|---|---|---|
| t検定 (t-test) |
|
|
|
|
| z検定 (z-test) |
|
|
|
|
| カイ二乗検定 (Chi-square test) |
|
|
|
|
| 分散分析 (ANOVA) |
|
|
|
|
表2: 主な検定手法の比較
3. 応用例
3.1. ビジネスアナリティクス
企業では、売上データの分析や顧客行動の予測などに統計手法が活用されています。例えば、Eコマースサイトでは、購買履歴データから顧客の嗜好を分析し、レコメンデーションシステムに活用しています。単回帰分析や重回帰分析を用いて売上予測を行い、意思決定に役立てています。
3.2. 品質管理
製造業では、品質管理のために統計的プロセス管理(SPC)が広く用いられています。製品の不良率低減や工程の安定化のために、管理図による監視や実験計画法による最適条件の探索が行われています。特に、t検定やカイ二乗検定を用いて製造プロセスの改善効果を統計的に検証することが一般的です。
3.3. 機械学習・人工知能
機械学習アルゴリズムの多くは統計学を基盤としています。回帰分析は予測モデルの基礎となり、主成分分析は次元削減技術として活用されています。また、モデルの評価や選択においても、p値や標準偏差などの統計的指標が重要な役割を果たしています。
3.4. 医療・疫学研究
新薬の開発や医療技術の評価には、臨床試験のデータを統計的に分析することが不可欠です。疫学研究では、特定の要因と疾病発生の関連を調査するために、ロジスティック回帰分析や生存分析などの統計手法が用いられています。有意水準を適切に設定し、第1種および第2種の誤りのリスクを管理することが特に重要です。
4. 例題
以下では、統計の基本的な概念から応用的な内容まで、段階的に理解を深めるための例題を提示します。
例題1:代表値とばらつき
あるプログラミング試験の10名の得点データが以下のように得られました:65, 70, 70, 75, 80, 80, 85, 85, 90, 95
この得点データの平均値、中央値、最頻値、分散、標準偏差を求めてください。
平均値 = (65+70+70+75+80+80+85+85+90+95)/10 = 795/10 = 79.5
中央値 = (80+80)/2 = 80(偶数個のデータなので中央の2つの平均)
最頻値 = 70, 80, 85(それぞれ2回出現)
分散 = [(65-79.5)²+(70-79.5)²+(70-79.5)²+(75-79.5)²+(80-79.5)²+(80-79.5)²+(85-79.5)²+(85-79.5)²+(90-79.5)²+(95-79.5)²]/10 = 87.25
標準偏差 = √87.25 ≈ 9.34
例題2:相関と回帰
あるWebサイトについて、広告費(万円)とアクセス数(千人)のデータが以下のように得られました:
| 広告費(x) | 10 | 15 | 20 | 25 | 30 |
|---|---|---|---|---|---|
| アクセス数(y) | 20 | 24 | 28 | 31 | 36 |
このデータから相関係数を求め、回帰直線を導出してください。また、広告費が22万円の場合のアクセス数を予測してください。
平均値: x̄ = (10+15+20+25+30)/5 = 20, ȳ = (20+24+28+31+36)/5 = 27.8
共分散の計算:
Cov(x,y) = [(10-20)(20-27.8)+(15-20)(24-27.8)+(20-20)(28-27.8)+(25-20)(31-27.8)+(30-20)(36-27.8)]/5
= [(-10)(-7.8)+(-5)(-3.8)+(0)(0.2)+(5)(3.2)+(10)(8.2)]/5
= [78+19+0+16+82]/5 = 195/5 = 39
分散の計算:
Vx = [(10-20)²+(15-20)²+(20-20)²+(25-20)²+(30-20)²]/5 = [100+25+0+25+100]/5 = 250/5 = 50
Vy = [(20-27.8)²+(24-27.8)²+(28-27.8)²+(31-27.8)²+(36-27.8)²]/5
= [60.84+14.44+0.04+10.24+67.24]/5 = 152.8/5 = 30.56
相関係数:
r = Cov(x,y)/(√Vx・√Vy) = 39/(√50・√30.56) = 39/39.06 ≈ 0.998
回帰直線:
y = a + bx
ここで、b = Cov(x,y)/Vx = 39/50 = 0.78
a = ȳ – b・x̄ = 27.8 – 0.78・20 = 27.8 – 15.6 = 12.2
したがって、y = 12.2 + 0.78x
広告費が22万円の場合のアクセス数の予測値:
y = 12.2 + 0.78・22 = 12.2 + 17.16 = 29.36(千人)
例題3:仮説検定
あるプログラムの処理時間について、改良前と改良後のデータが以下のように得られました:
改良前:平均処理時間 μ1 = 45秒, 標準偏差 σ1 = 5秒, サンプルサイズ n1 = 30 改良後:平均処理時間 μ2 = 42秒, 標準偏差 σ2 = 4秒, サンプルサイズ n2 = 30
有意水準5%で、処理時間が改良によって短縮されたかどうかを検定してください。
帰無仮説 H0:μ1 = μ2(改良による効果はない)
対立仮説 H1:μ1 > μ2(改良により処理時間が短縮された)
検定統計量
z = (μ1 – μ2)/√(σ1²/n1 + σ2²/n2)
= (45 – 42)/√(5²/30 + 4²/30)
= 3/√(25/30 + 16/30)
= 3/√(41/30) = 3/1.17 ≈ 2.56
z検定を用いる場合、有意水準5%の棄却域は z > 1.645
計算された検定統計量 z = 2.56 > 1.645 であるため、帰無仮説は棄却されます。
p値 = P(Z > 2.56) ≈ 0.0052 < 0.05
したがって、有意水準5%において、改良によって処理時間が統計的に有意に短縮されたと結論づけられます。
5. まとめ
本記事では、応用情報技術者試験シラバスの「統計」に含まれる重要な概念について解説しました。
統計学の基本的な概念である度数分布表やヒストグラム、代表値(平均値、中央値、最頻値)、ばらつきの指標(分散、標準偏差、歪度、尖度)について理解することが重要です。
また、相関分析や回帰分析などの手法を用いて、変数間の関係を定量的に評価できるようになることも求められます。さらに、多変量解析手法(主成分分析、因子分析)や、データの尺度(名義尺度、順序尺度、間隔尺度、比例尺度)についても理解が必要です。
統計的推測の基礎となる推定(点推定、区間推定)の考え方や、尤度、最尤推定の概念を把握することも重要です。仮説検定においては、帰無仮説と対立仮説の設定、有意水準、p値、棄却域といった基本的な概念や、第1種・第2種の誤り、検出力についての理解が求められます。また、具体的な検定手法(t検定、z検定、カイ二乗検定など)の特徴と適用場面についても押さえておく必要があります。
これらの統計的知識は、情報処理技術者として実際のデータ分析やシステム開発において、適切な意思決定を行うための重要な基盤となります。

