1. 概要
確率論は、不確実性を数学的に扱うための基礎理論です。応用情報処理技術者として、確率の概念を理解することは、アルゴリズムの分析、データサイエンス、AI、セキュリティなど多くの分野で重要となります。本記事では、順列や組合せといった数え上げの基礎から、確率の基本定理、様々な確率分布、そしてマルコフ過程まで体系的に解説します。これらの知識は、システム設計や問題解決において不確実性を扱う際の理論的基盤となります。
2. 詳細説明
2.1. 数え上げの基礎
2.1.1. 順列
順列とは、n個のものからr個を選び、それを並べる場合の数を表します。順序が重要であり、nPrと表記します。
$$nPr = \frac{n!}{(n-r)!}$$
ここで、n!は階乗を表し、n! = n × (n-1) × (n-2) × … × 2 × 1 で計算されます。例えば、5! = 5 × 4 × 3 × 2 × 1 = 120 です。
2.1.2. 組合せ
組合せとは、n個のものからr個を選ぶ場合の数を表します。順序は考慮せず、nCrと表記します。
$$nCr = \frac{n!}{r!(n-r)!}$$
2.1.3. 場合の数
場合の数を求める際には、以下の法則が重要です:
- 加法定理: 互いに排反な事象A, Bについて、「AまたはB」の場合の数は、Aの場合の数とBの場合の数の和になります。
- 乗法定理: 複数の選択を順番に行う場合、全体の場合の数は各選択肢の場合の数の積になります。
2.2. 確率の基本
2.2.1. 確率の定義
事象Aの確率P(A)は、全事象の場合の数に対する事象Aの場合の数の比として定義されます:
$$P(A) = \frac{\text{事象Aの場合の数}}{\text{全事象の場合の数}}$$
確率は0から1の間の値をとります。
2.2.2. 確率の基本定理
- 加法定理: P(A∪B) = P(A) + P(B) – P(A∩B)
- 乗法定理: P(A∩B) = P(A) × P(B|A) = P(B) × P(A|B)
ここで、P(A∩B)は同時確率、P(B|A)は条件付き確率を表します。条件付き確率とは、事象Aが起きたという条件下での事象Bの確率です。
2.2.3. ベイズの定理
ベイズの定理は、原因と結果の確率関係を表す重要な定理です:
$$P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}$$
この定理は機械学習やデータ分析において特に重要です。
2.3. 確率分布
2.3.1. 離散型確率分布
- ベルヌーイ分布: 成功確率pの試行を1回行った結果を表します。
- 二項分布: 成功確率pの試行をn回独立に行った時の成功回数を表します。期待値はnp、分散はnp(1-p)です。
- ポアソン分布: 一定時間内に発生する事象の回数を表します。期待値と分散は同じ値λです。
2.3.2. 連続型確率分布
連続型確率分布では、確率密度関数を用いて確率を表現します。
- 正規分布: 平均μ、標準偏差σの釣鐘型の分布で、多くの自然現象に当てはまります。
- 指数分布: 事象間の待ち時間など、ポアソン過程における時間間隔を表します。
- カイ二乗分布: 正規分布に従う確率変数の平方和の分布で、統計的検定に利用されます。
2.3.3. 期待値
確率変数Xの期待値E[X]は、各値に確率を掛けて足し合わせたものです:
- 離散型の場合: E[X] = Σ x_i × P(X = x_i)
- 連続型の場合: E[X] = ∫ x × f(x) dx(fは確率密度関数)
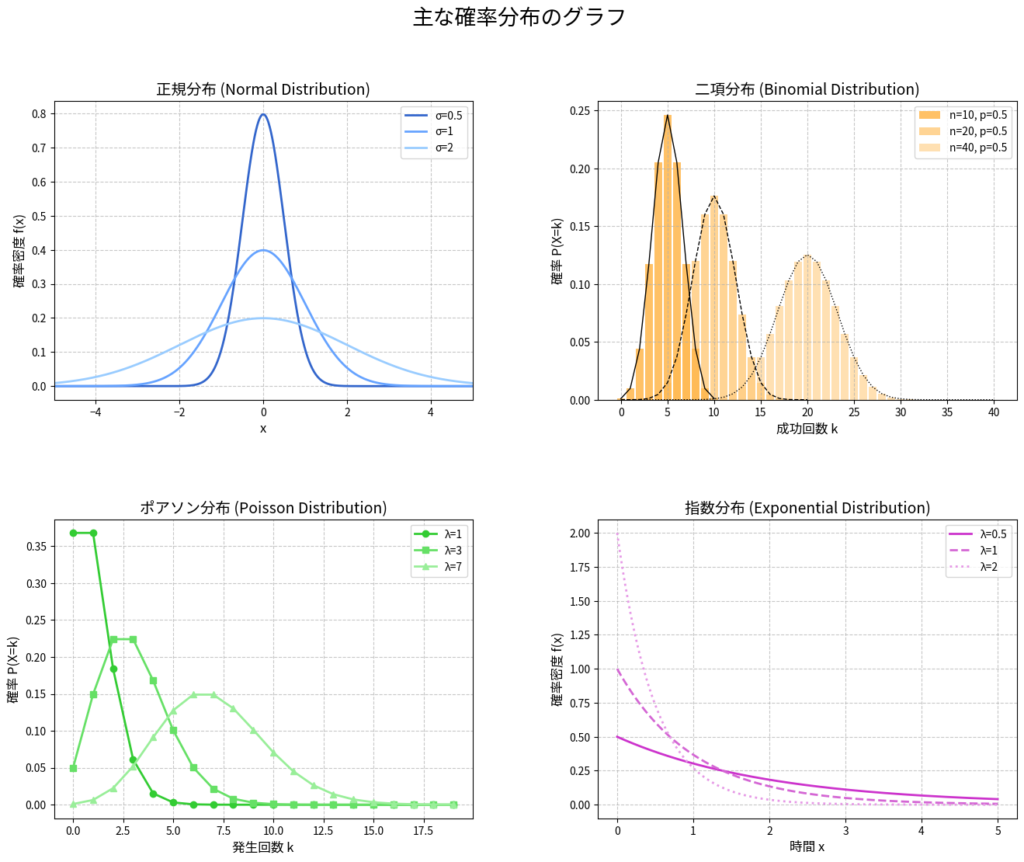
図2: 主な確率分布のグラフ
| 分布名 | 確率(密度)関数 | 期待値 | 分散 | 特徴 | 応用例 |
|---|---|---|---|---|---|
| ベルヌーイ分布 | P(X=1) = p P(X=0) = 1-p |
p | p(1-p) | 成功/失敗の2値のみをとる試行 | コイン投げ、Yes/No質問 |
| 二項分布 | P(X=k) = nCk pk(1-p)n-k | np | np(1-p) | n回の独立したベルヌーイ試行での成功回数 | 品質管理、テスト結果の分析 |
| ポアソン分布 | P(X=k) = e-λλk/k! | λ | λ | 一定期間内に発生する事象の回数 | サーバーアクセス数、障害発生数 |
| 正規分布 | f(x) = (1/√(2πσ²))e-(x-μ)²/(2σ²) | μ | σ² | 釣鐘型の分布、多くの自然現象に適合 | 身長・体重などの人間の特性、測定誤差 |
| 指数分布 | f(x) = λe-λx (x≥0) | 1/λ | 1/λ² | 無記憶性を持つ、待ち時間のモデル | 機器の寿命、サービス時間 |
| カイ二乗分布 | 複雑な形式(自由度kに依存) | k | 2k | 正規分布に従う変数の二乗和の分布 | 適合度検定、独立性の検定 |
表1: 主な確率分布の特徴まとめ
2.4. マルコフ過程
マルコフ過程とは、将来の状態が現在の状態にのみ依存し、過去の状態には依存しないような確率過程です。これは「無記憶性」と呼ばれる特性を持ちます。マルコフ連鎖はマルコフ過程の一種で、離散的な状態空間を持つものを指します。
3. 応用例
3.1. 情報セキュリティにおける応用
暗号技術において、確率論は鍵の強度や攻撃成功確率の分析に使用されます。例えば、総当たり攻撃の成功確率はベルヌーイ試行としてモデル化できます。
3.2. 通信システムにおける応用
通信エラーの発生確率はポアソン分布でモデル化されることが多く、誤り訂正符号の設計に応用されます。また、ネットワークのトラフィック予測にも確率モデルが使われます。
3.3. AIと機械学習における応用
ベイズの定理は機械学習の基礎となっており、ナイーブベイズ分類器やベイジアンネットワークに応用されています。また、マルコフ過程は隠れマルコフモデル(HMM)として音声認識や自然言語処理に利用されています。
3.4. システム信頼性工学における応用
システムの故障率や平均故障間隔(MTBF)は指数分布でモデル化されることが多く、信頼性評価に使われます。
4. 例題
例題1: 順列と組合せ
Aさん、Bさん、Cさん、Dさん、Eさんの5人から委員長、副委員長、書記の3人を選ぶ方法は何通りありますか?
役職の順序があるため、これは順列の問題です。
5P3 = 5!/(5-3)! = 5!/2! = 5 × 4 × 3 = 60通り
例題2: 確率の基本
袋の中に赤玉3個、白玉2個、青玉4個が入っています。この中から2個の玉を同時に取り出すとき、(1)両方とも赤玉である確率、(2)同じ色の玉である確率を求めなさい。
全体の場合の数: 9C2 = 9!/(2! × 7!) = 36通り
(1) 両方とも赤玉である確率:
赤玉を2個選ぶ場合の数: 3C2 = 3通り P(両方赤) = 3/36 = 1/12
(2) 同じ色の玉である確率:
赤玉2個: 3C2 = 3通り
白玉2個: 2C2 = 1通り
青玉2個: 4C2 = 6通り
同じ色の玉を引く場合の数: 3 + 1 + 6 = 10通り
P(同じ色) = 10/36 = 5/18
例題3: 条件付き確率とベイズの定理
あるソフトウェアのバグ検出テストがあります。実際にバグがある場合、テストでバグを検出する確率は0.9です。一方、バグがない場合に誤ってバグがあると判定する確率は0.05です。ソフトウェアにバグがある確率が0.2だとすると、テストでバグが検出されたとき、実際にバグがある確率を求めなさい。
A: ソフトウェアにバグがある事象
B: テストでバグが検出される事象
求めたいのは条件付き確率P(A|B)です。
P(A) = 0.2(バグがある確率)
P(B|A) = 0.9(バグがある場合にテストで検出される確率)
P(B|¬A) = 0.05(バグがない場合に誤検出する確率)
P(¬A) = 1 – P(A) = 0.8(バグがない確率)
ベイズの定理より:
P(A|B) = P(B|A) × P(A) / P(B)
P(B) = P(B|A) × P(A) + P(B|¬A) × P(¬A) = 0.9 × 0.2 + 0.05 × 0.8 = 0.18 + 0.04 = 0.22
したがって、P(A|B) = 0.9 × 0.2 / 0.22 = 0.18 / 0.22 = 0.82
つまり、テストでバグが検出されたとき、実際にバグがある確率は約82%です。
例題4: 確率分布と期待値
あるWebサーバーに1分間にアクセスがある回数は平均5回のポアソン分布に従うとします。
(1)1分間にアクセスがない確率
(2)1分間に3回以上アクセスがある確率
(3)アクセス間の平均時間間隔
を求めなさい。
λ = 5(1分間あたりの平均アクセス回数)
(1) 1分間にアクセスがない確率:
ポアソン分布の確率質量関数: P(X = k) = e^(-λ) × λ^k / k!
P(X = 0) = e^(-5) × 5^0 / 0! = e^(-5) ≈ 0.0067
(2) 1分間に3回以上アクセスがある確率:
P(X ≥ 3) = 1 – P(X < 3) = 1 – [P(X = 0) + P(X = 1) + P(X = 2)]
P(X = 1) = e^(-5) × 5^1 / 1! = 5e^(-5) ≈ 0.0337
P(X = 2) = e^(-5) × 5^2 / 2! = 25e^(-5) / 2 ≈ 0.0842
P(X ≥ 3) = 1 – (0.0067 + 0.0337 + 0.0842) ≈ 1 – 0.1246 ≈ 0.8754
(3) アクセス間の平均時間間隔:
ポアソン過程におけるイベント間の時間間隔は指数分布に従い、その期待値は1/λです。
平均時間間隔 = 1/5 分 = 0.2 分 = 12 秒
例題5: マルコフ過程
あるシステムが「正常」、「警告」、「エラー」の3つの状態をとるとします。1時間後の状態遷移確率が以下の遷移行列で与えられているとき、現在「正常」状態にあるシステムが2時間後に「エラー」状態である確率を求めなさい。
| 現在/1時間後 | 正常 | 警告 | エラー |
|---|---|---|---|
| 正常 | 0.7 | 0.2 | 0.1 |
| 警告 | 0.3 | 0.4 | 0.3 |
| エラー | 0.2 | 0.3 | 0.5 |
表2: 例題5のマルコフ遷移行列
解答例:
2時間後の遷移確率は行列の2乗P^2で表されます。
P^2を計算すると:
P^2 = [0.58 0.26 0.16]
[0.37 0.34 0.29]
[0.31 0.33 0.36]
現在「正常」状態なので、1行目を見ます。2時間後に「エラー」状態である確率は0.16(16%)です。
5. まとめ
本記事では、応用情報処理技術者試験で必要とされる確率の基礎理論について説明しました。
- 数え上げの基礎: 順列、組合せ、場合の数の求め方と、加法定理・乗法定理の適用
- 確率の基本: 確率の定義、加法定理、乗法定理、同時確率、条件付き確率、ベイズの定理
- 確率分布: 離散型(ベルヌーイ分布、二項分布、ポアソン分布)と連続型(正規分布、指数分布、カイ二乗分布)の確率分布と確率密度関数、期待値の計算
- マルコフ過程: 無記憶性を持つ確率過程の特性と遷移確率行列による状態予測
これらの概念は、情報処理の様々な分野で応用されており、特にAI、機械学習、セキュリティ、信頼性工学などの理解に不可欠です。応用情報処理技術者として、これらの確率論の基礎を身につけることで、より効果的なシステム設計や問題解決ができるようになるでしょう。

