1. M/M/1モデルとは何か
M/M/1モデルは、待ち行列理論の基本的なモデルで、1台のサーバにランダムに顧客が到着し、サービスを受けるシステムを表します。名前の意味は次の通りです:
- 最初のM: 到着過程がマルコフ性(指数分布)に従うことを示します
- 2番目のM: サービス過程がマルコフ性(指数分布)に従うことを示します
- 1: サーバが1台であることを示します
2. 指数分布とは
M/M/1モデルを理解するためには、指数分布の特性を知ることが重要です。指数分布は「無記憶性」という特殊な性質を持ちます。これは「過去の経過時間に関係なく、次の事象が発生するまでの残り時間の確率分布が同じ」という性質です。
例: コンビニのレジで5分待っている人がいるとします。指数分布に従うなら、この人がさらに2分待つ確率は、今レジに到着した人が2分待つ確率と同じです。つまり、すでに待った時間は関係ありません。
この特性により、M/M/1モデルは数学的に扱いやすくなります。
3. M/M/1モデルの直感的な理解
3.1. 安定条件(ρ < 1)の意味
システム利用率 ρ = λ/μ が1未満である必要があります。これは何を意味するのでしょうか?
直感的に考えると:
- λ: 1時間あたりに10人が来店する
- μ: 1時間あたりに15人を処理できる
この場合、ρ = 10/15 = 0.67 となり、サーバの処理能力が到着率を上回っているため、システムは安定しています。
逆に、λ = 20人/時間、μ = 15人/時間とすると、ρ = 20/15 = 1.33 > 1 となり、処理しきれない顧客が徐々に蓄積され、待ち行列は無限に増加してしまいます。
3.2. 各計算式の関係性
M/M/1モデルの各指標は互いに関連しています:
- システム利用率(ρ)= λ/μ:サーバがどれだけ忙しいかを表します。例えばρ = 0.8なら、サーバは時間の80%が稼働中で、20%は待機中です。
- 平均システム内顧客数(L)= ρ/(1-ρ):この式はなぜこうなるのでしょう?
- ρが大きくなると(1に近づくと)、分母が小さくなるので、L値は急激に増加します
- ρ = 0.5なら、L = 0.5/(1-0.5) = 1人
- ρ = 0.9なら、L = 0.9/(1-0.9) = 9人
- つまり、システム利用率が90%になると、平均顧客数は9倍になります!
- 平均待ち行列長(Lq)= ρ²/(1-ρ):サービス中の顧客を除いた待ち行列の長さ
- L = Lq + ρ となることに注目(システム内顧客 = 待ち行列 + サービス中)
- 平均システム内滞在時間(W)= 1/(μ-λ):
- 分母の (μ-λ) は「余剰サービス能力」と考えられます
- 余剰能力が少ないほど、滞在時間は長くなります
- 平均待ち時間(Wq)= ρ/(μ-λ):
- W = Wq + 1/μ となることに注目(滞在時間 = 待ち時間 + サービス時間)
4. 具体例で理解する
例:コンビニのレジ
あるコンビニでは、平均して3分に1人の割合で顧客が来店し(λ = 0.33人/分)、レジ処理には平均2分かかる(μ = 0.5人/分)とします。
- システム利用率:ρ = λ/μ = 0.33/0.5 = 0.66 → レジ店員は時間の66%を顧客対応に費やしている
- 平均待ち行列長:Lq = ρ²/(1-ρ) = 0.66²/(1-0.66) = 0.44/0.34 ≈ 1.29人 → 平均して約1.3人が待っている
- 平均システム内顧客数:L = ρ/(1-ρ) = 0.66/0.34 ≈ 1.94人 → 平均して約1.9人がシステム内(待機中+レジ処理中)にいる
- 平均待ち時間:Wq = ρ/(μ-λ) = 0.66/(0.5-0.33) ≈ 3.88分 → 顧客は平均約3.9分待つ
- 平均システム内滞在時間:W = 1/(μ-λ) = 1/(0.5-0.33) ≈ 5.88分 → 顧客は平均約5.9分システム内にいる(待ち時間+レジ処理時間)
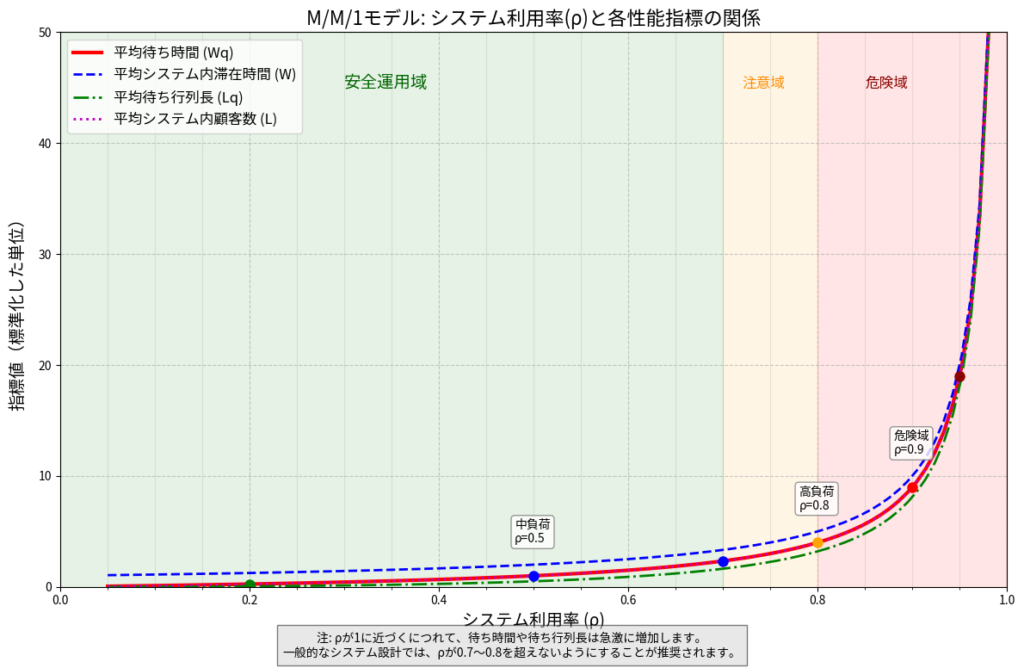
ρ(システム利用率)の影響を見る
同じコンビニで、繁忙期になり顧客の到着率が増加した場合:
| λ(人/分) | ρ = λ/μ | 平均待ち行列長 Lq | 平均待ち時間 Wq(分) |
|---|---|---|---|
| 0.25 | 0.5 | 0.5 | 2 |
| 0.33 | 0.66 | 1.29 | 3.88 |
| 0.4 | 0.8 | 3.2 | 8 |
| 0.45 | 0.9 | 8.1 | 18 |
| 0.49 | 0.98 | 48 | 98 |
ρが1に近づくにつれて待ち時間が急激に増加することが分かります!
5. M/M/1モデルの重要な性質
- 指数関数的な悪化:システム利用率ρが1に近づくと、待ち時間や待ち行列長は指数関数的に増加します。そのため、高負荷状態(ρ > 0.8)での運用は避けるべきです。
- 到着分布の形状:M/M/1モデルでは、連続する到着の間隔は指数分布に従います。これは、短い間隔で到着が集中したり(バースト)、長い間隔が生じたりする可能性があることを意味します。
- リトルの法則との関係:M/M/1モデルはリトルの法則(L = λW, Lq = λWq)を満たします。これは、M/M/1だけでなく、多くの待ち行列モデルに適用できる普遍的な法則です。
6. M/M/1モデルをよりよく理解するためのポイント
- 直感に反する結果:システム利用率が90%の場合、待ち時間は利用率50%の場合の9倍になります。システムの効率を高めすぎると、かえって顧客の待ち時間が長くなることがあります。
- 余裕を持った設計:実用的なシステム設計では、ピーク時でもρが0.7〜0.8を超えないようにするのが一般的です。
- 変動の影響:実際のシステムでは、到着率やサービス率が時間とともに変動することがあります。そのため、平均だけでなく、変動も考慮することが重要です。
7. 計算式の覚え方と関連性
計算式を丸暗記するのではなく、関連性を理解すると覚えやすくなります:
- 基本は ρ = λ/μ (システム利用率)
- L = ρ/(1-ρ) (平均システム内顧客数)
- ρが1に近づくと分母が小さくなり、L値が大きくなることをイメージ
- Lq = ρ²/(1-ρ) (平均待ち行列長)
- L = Lq + ρ の関係を覚える
- つまり、Lq = L – ρ = ρ/(1-ρ) – ρ = ρ²/(1-ρ)
- W = 1/(μ-λ) (平均システム内滞在時間)
- 分母の (μ-λ) は「余剰処理能力」と考える
- Wq = ρ/(μ-λ) (平均待ち時間)
- W = Wq + 1/μ の関係を覚える
- つまり、Wq = W – 1/μ = 1/(μ-λ) – 1/μ = ρ/(μ-λ)
これらの指標は互いに密接に関連しており、1つの指標から他の指標を導くことができます。
8. 実用的な考え方
応用情報処理技術者試験では、計算問題としてM/M/1モデルが出題されることが多いですが、実際のシステム設計では次のような考え方が重要です:
- 十分な余裕:理論上はρ < 1なら安定ですが、実際には余裕を持ってρ < 0.8程度に設計します。
- ピーク時の考慮:平均到着率だけでなく、ピーク時の到着率も考慮する必要があります。
- バースト対応:短時間に顧客が集中する「バースト」に対応できるよう、バッファを設計します。
- トレードオフ:リソース(サーバ数)を増やすとコストが上がりますが、待ち時間は減少します。最適な設計はこのトレードオフを考慮します。
9. 待ち行列理論シミュレーション
10. まとめ
M/M/1モデルは、待ち行列理論の基本となるモデルです。単なる計算式の暗記ではなく、各パラメータの意味や関連性を理解することが重要です。特に、システム利用率ρが1に近づくにつれて待ち時間が急激に増加するという性質は、実際のシステム設計においても重要な洞察を与えます。
応用情報処理技術者試験での出題では、これらの概念を理解した上で、与えられたパラメータから必要な指標を計算できることが求められます。計算式の意味を理解していれば、暗記に頼らずとも問題に対応できるようになります。

