1. はじめに
線形計画法(Linear Programming、LP)は、限られた資源を最適に配分するための数学的手法です。実社会における意思決定問題を解決するための強力なツールであり、経済学、経営学、工学など多岐にわたる分野で応用されています。
線形計画法の特徴は、目的関数と制約条件がすべて線形(一次式)であることです。例えば、限られた予算内で最大の効果を得る、限られた材料で最大の利益を上げる、最小のコストで必要な栄養素を摂取するなど、日常から産業まで様々な最適化問題を解くことができます。
実社会での応用例としては以下のようなものがあります。
- 製造業における生産計画
- 物流における輸送経路の最適化
- 金融における投資ポートフォリオの最適化
- 農業における栽培計画
- 医療におけるリソース配分
| 応用分野 | 具体的な問題例 | 特徴 | 実世界での適用例 |
|---|---|---|---|
| 製造業 |
– 製品ミックス問題 – 生産計画最適化 – 工程計画 |
限られた資源(原材料、機械、労働力)を最適に配分し、利益を最大化 | 自動車メーカーの部品調達、電子機器の製造ライン最適化 |
| 物流・輸送 |
– 輸送問題 – 経路最適化 – 配送計画 |
複数の供給地から複数の需要地への最小コスト輸送経路の決定 | Amazon等の配送センター配置、物流会社の配送ルート最適化 |
| 金融工学 |
– ポートフォリオ最適化 – 資産配分問題 – リスク管理 |
期待リターンを確保しながらリスクを最小化する投資配分の決定 | 投資信託の資産配分、年金基金の運用、リスクヘッジ戦略 |
| エネルギー管理 |
– 電力需給計画 – エネルギーミックス – 発電所運用計画 |
需要を満たしながら発電コストや環境負荷を最小化 | 電力会社の電源構成最適化、スマートグリッドの需給調整 |
| 農業 |
– 作付け計画 – 灌漑計画 – 収穫スケジュール |
土地や水などの限られた資源を最適に利用し、収益を最大化 | 大規模農場の作付け計画、効率的な水資源利用計画 |
| 人的資源管理 |
– シフトスケジューリング – 人員配置 – プロジェクト割当 |
必要なスキルと人員制約を考慮した最適な人材配置 | コールセンターのシフト管理、病院のナーススケジューリング |
| 医療・ヘルスケア |
– 医療資源配分 – 栄養計画 – 治療計画最適化 |
限られた医療資源を効率的に配分し、患者の健康アウトカムを最大化 | 病院のベッド配分、透析センターのスケジューリング、最小コストでの栄養要件充足 |
| 広告・マーケティング |
– メディアミックス最適化 – 広告予算配分 – 市場セグメント戦略 |
限られた予算でリーチやコンバージョンを最大化する広告配分 | デジタルマーケティングのチャネル最適化、広告キャンペーンのROI最大化 |
図表1: 線形計画法の応用分野一覧表
2. 線形計画法の基礎
2.1. 定義と基本的な考え方
線形計画法とは、線形の制約条件の下で線形の目的関数を最大化または最小化する問題を解く手法です。その数学的定式化は次のようになります。
目的関数(最大化または最小化したい関数):
$$z = c_1x_1 + c_2x_2 + \ldots + c_nx_n$$
制約条件(守るべき条件):
$$a_{11}x_1 + a_{12}x_2 + \ldots + a_{1n}x_n \leq b_1$$ $$a_{21}x_1 + a_{22}x_2 + \ldots + a_{2n}x_n \leq b_2$$ $$\vdots$$ $$a_{m1}x_1 + a_{m2}x_2 + \ldots + a_{mn}x_n \leq b_m$$
非負制約(変数の条件):
$$x_1, x_2, \ldots, x_n \geq 0$$
ここで、
- $x_1, x_2, \ldots, x_n$ は決定変数
- $c_1, c_2, \ldots, c_n$ は目的関数の係数
- $a_{ij}$ は制約条件の係数
- $b_1, b_2, \ldots, b_m$ は制約条件の右辺の値
2.2. 実行可能領域の概念
線形計画問題において、すべての制約条件を満たす点の集合を「実行可能領域」と呼びます。2次元や3次元の問題では、この実行可能領域は多角形または多面体として表現できます。線形計画法の重要な性質として、最適解は実行可能領域の頂点に存在することが証明されています。
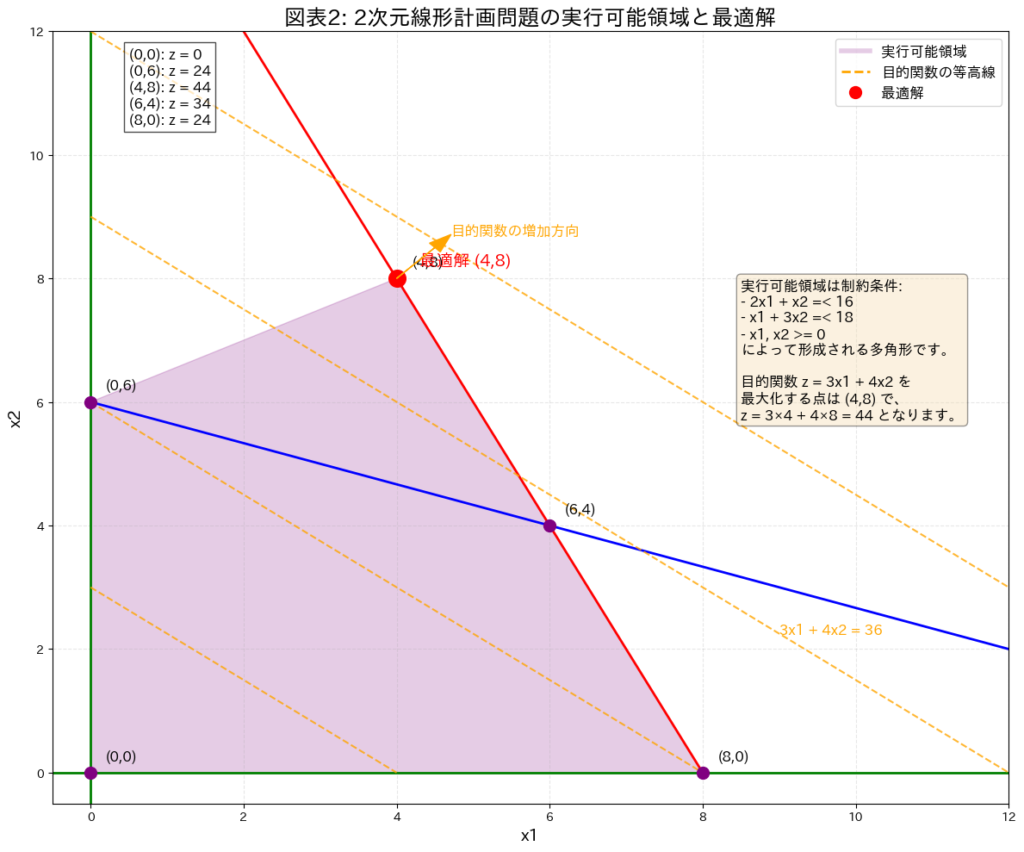
図表2: 2次元線形計画問題の実行可能領域と最適解
2.3. 線形計画法の基本用語解説
- 基底解(Basic Solution): シンプレックス法で扱う特殊な解で、$n$個の変数のうち最大$m$個(制約式の数)だけが正の値を持ち、残りは0となる解です。
- 基底変数(Basic Variable): 基底解において正の値を持つ変数のこと。
- 非基底変数(Non-basic Variable): 基底解において値が0の変数のこと。
- 退化(Degeneracy): 基底解において、基底変数の中に値が0のものがある状態。
- ピボット操作(Pivoting): シンプレックス法で使われる基底変数と非基底変数を入れ替える操作。
3. 線形計画問題の標準形
線形計画問題を解くアルゴリズムを適用するためには、問題を「標準形」に変換する必要があります。標準形は以下のように定義されます。
- 目的関数は最大化(または最小化)の形式
- すべての制約条件が等式
- すべての変数が非負
flowchart TD
A[線形計画問題の初期形式] --> B{目的関数は
最大化形式か?}
B -->|Yes| C[目的関数はそのまま]
B -->|No| D[目的関数に(-1)を掛けて
最大化形式に変換]
C --> E{制約条件に
不等式があるか?}
D --> E
E -->|Yes| F{不等式は「≤」形式か?}
E -->|No| J[すべての制約条件は等式]
F -->|Yes| G[スラック変数を追加
ax + by ≤ c
→ ax + by + s = c]
F -->|No| H[「≥」形式の不等式にはサープラス変数を導入
ax + by ≥ c
→ ax + by - s = c]
G --> I{すべての不等式を\n処理したか?}
H --> I
I -->|No| F
I -->|Yes| J
J --> K{変数に非負制約
がないものがあるか?}
K -->|Yes| L[非負でない変数xを
2つの非負変数の差に分解
x = x⁺ - x⁻]
K -->|No| M[すべての変数は非負]
L --> N{すべての非負でない
変数を処理したか?}
N -->|No| L
N -->|Yes| M
M --> O[標準形の線形計画問題]
classDef process fill:#a3e4d7,stroke:#333,stroke-width:1px;
classDef decision fill:#d4efdf,stroke:#333,stroke-width:1px;
classDef startpoint fill:#f9e79f,stroke:#333,stroke-width:1px;
classDef endpoint fill:#f5cba7,stroke:#333,stroke-width:1px;
class A,G,H,L process;
class B,E,F,I,K,N decision;
class C,D,J,M process;
class O endpoint;
図表3: 標準形変換のフローチャート
3.1. 不等式制約から等式制約への変換
不等式制約は、スラック変数(余剰変数)やサープラス変数(超過変数)を導入することで等式制約に変換できます。
- 「$\leq$」型の制約にはスラック変数を加えて等式にします:
$$a_{i1}x_1 + a_{i2}x_2 + \ldots + a_{in}x_n \leq b_i$$ $$\Rightarrow a_{i1}x_1 + a_{i2}x_2 + \ldots + a_{in}x_n + s_i = b_i \quad (s_i \geq 0)$$ - 「$\geq$」型の制約にはサープラス変数を引いて等式にします:
$$a_{i1}x_1 + a_{i2}x_2 + \ldots + a_{in}x_n \geq b_i$$ $$\Rightarrow a_{i1}x_1 + a_{i2}x_2 + \ldots + a_{in}x_n – s_i = b_i \quad (s_i \geq 0)$$
3.2. 非負制約の扱い方
変数に非負制約がない場合、その変数を非負の2つの変数の差として表現できます。
$$x_j = x_j^+ – x_j^- \quad (x_j^+, x_j^- \geq 0)$$
4. 解法アルゴリズム
4.1. 図解法(2次元の場合)
2次元(変数が2つ)の線形計画問題は、座標平面上で図解的に解くことができます。
- 各制約条件を座標平面上の直線として描く
- それらの直線によって囲まれる領域(実行可能領域)を特定する
- 目的関数の等高線を描き、実行可能領域との最適な交点を見つける
4.2. シンプレックス法の基本原理
シンプレックス法は、ジョージ・ダンツィヒによって1947年に開発された線形計画問題を解くための効率的なアルゴリズムです。基本的なステップは以下の通りです。
- 線形計画問題を標準形に変換する
- 実行可能な初期基底解を見つける
- 現在の解を改善できる非基底変数を選ぶ(ピボット列の選択)
- 制約条件を満たしながら、その変数の値を増加させる(ピボット行の選択)
- 基底解を更新する
- 解が最適になるまで3〜5を繰り返す
シンプレックス法は、実行可能領域の頂点から隣接する頂点へと移動することで、目的関数の値を改善していきます。
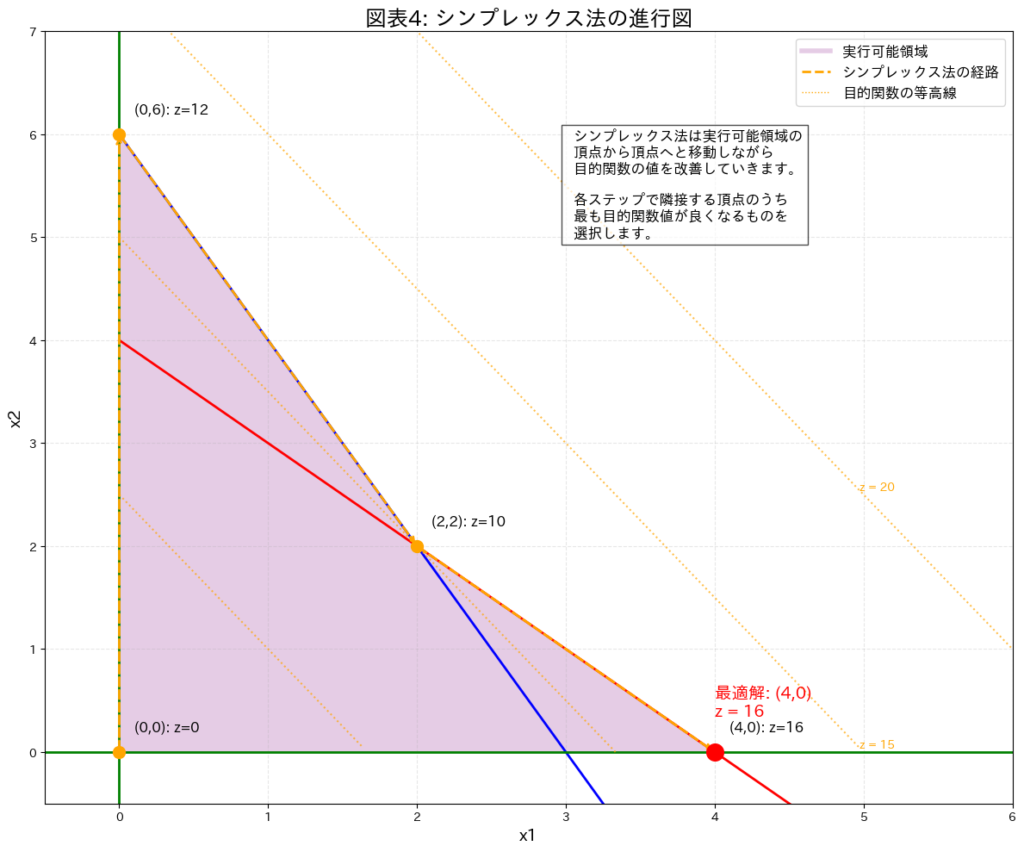
図表4: シンプレックス法の進行図
4.2.1. シンプレックス法の数値例
以下の線形計画問題を考えましょう。
最大化:
$z = 3x_1 + 2x_2$
制約条件:
- $x_1 + x_2 \leq 4$
- $2x_1 + x_2 \leq 6$
- $x_1, x_2 \geq 0$
まず、スラック変数 $s_1, s_2$ を導入して標準形に変換します:
$x_1 + x_2 + s_1 = 4$ $2x_1 + x_2 + s_2 = 6$ $z – 3x_1 – 2x_2 = 0$
初期の基底解は $(x_1, x_2, s_1, s_2) = (0, 0, 4, 6)$、目的関数値は $z = 0$ です。
1回目のピボット操作:$x_1$ を基底変数に入れる $x_1 = 2 – \frac{1}{2}x_2 – \frac{1}{2}s_2$ $s_1 = 2 – x_2 + \frac{1}{2}s_2$ $z = 6 – \frac{1}{2}x_2 – \frac{3}{2}s_2$
新しい基底解は $(x_1, x_2, s_1, s_2) = (3, 0, 1, 0)$、目的関数値は $z = 9$ です。
このプロセスを繰り返し、最終的に最適解を求めます。
4.3. 内点法の概要
内点法は、実行可能領域の内部を通って最適解に到達するアルゴリズムです。大規模な線形計画問題に対して効率的であり、以下の特徴があります。
- 実行可能領域の内部から開始する
- 目的関数の勾配方向に沿って移動する
- 境界に近づくと障壁関数を使って内部にとどまるよう調整する
- 解が最適解に収束するまで繰り返す
4.4. 解法アルゴリズムの比較
| アルゴリズム | 基本原理 | 特徴 | 長所 | 短所 | 適した問題規模・特性 |
|---|---|---|---|---|---|
| 図解法 | 制約条件を図示し、実行可能領域の頂点で目的関数を評価する |
– 幾何学的アプローチ – 視覚的に理解しやすい – 手計算で可能 |
– 原理が直感的に理解しやすい – 教育目的に最適 – 解の過程が視覚的に確認できる |
– 2次元(変数2つ)または3次元までしか適用できない – 制約条件が多いと図が複雑になる |
– 変数が2つまでの小規模問題 – 教育・学習目的の問題 |
| シンプレックス法 | 実行可能領域の頂点から隣接する頂点へと移動しながら目的関数を改善する |
– 代数的アプローチ – 反復的なピボット操作 – 実行可能解から開始する |
– 多くの実用的な問題で効率的 – 数値的に安定している – 最終的に厳密解を得られる |
– 最悪の場合、計算時間が問題サイズに対して指数関数的に増加 – 初期実行可能解の構築が必要 – サイクリングの可能性がある |
– 中小規模の問題(数百変数程度まで) – 疎行列(ゼロ要素が多い)問題 – 精度が重要な問題 |
| 内点法 | 実行可能領域の内部を通じて最適解に到達する |
– 多項式時間アルゴリズム – 障壁関数を利用 – 内部点から開始する |
– 大規模問題に効率的 – 最悪計算時間の理論的保証がある – 問題の構造を活用しやすい |
– 実装が複雑 – 精度に関する問題が生じることがある – 感度分析がシンプレックス法より難しい |
– 大規模問題(数千〜数百万変数) – 密行列問題 – 高い精度が必要でない問題 |
| 楕円体法 | 実行可能領域を含む楕円体を繰り返し縮小させて最適解に近づける |
– 多項式時間アルゴリズム – 理論的に優れた計算量 – カーマーカーの方法の前身 |
– 理論的に保証された多項式時間 – 初期実行可能解が不要 – 双対定理の証明に役立つ |
– 実用性が低い – 計算量の定数項が大きい – 数値的に不安定になりやすい |
– 理論的研究 – 特殊な構造を持つ問題 |
| 遺伝的アルゴリズム (近似解法) |
自然淘汰のプロセスを模倣し、解の集団を進化させる |
– メタヒューリスティック手法 – 多様な解の探索 – 局所最適解から脱出できる |
– 複雑な問題に対応可能 – グローバル最適解を見つける可能性が高い – 並列処理に適している |
– 厳密解の保証がない – パラメータ調整が必要 – 計算コストが高い |
– 非凸や非線形要素を含む複雑な問題 – 近似解で十分な問題 – 多目的最適化問題 |
図表5: 解法アルゴリズムの比較表
5. 代表的な応用分野
5.1. 生産計画と資源配分
製造業では、限られた資源(機械、労働力、原材料など)を使って利益を最大化するための生産計画に線形計画法が活用されます。
例:製品ミックス問題
家具メーカーがテーブルと椅子を製造しているとします。テーブル1台の利益は10,000円、椅子1脚の利益は3,000円です。テーブル1台の製造には木材10単位と労働時間8時間が必要で、椅子1脚には木材3単位と労働時間2時間が必要です。利用可能な木材は100単位、労働時間は80時間のとき、利益を最大化する製品ミックスを求めます。
数式化:
- 決定変数:テーブルの製造数$x_1$、椅子の製造数$x_2$
- 目的関数(利益最大化):$\max z = 10000x_1 + 3000x_2$
- 制約条件:
- 木材:$10x_1 + 3x_2 \leq 100$
- 労働時間:$8x_1 + 2x_2 \leq 80$
- 非負制約:$x_1, x_2 \geq 0$
5.2. 輸送問題とネットワークフロー
複数の供給地から複数の需要地への輸送を最適化する問題も線形計画法で解くことができます。
例:輸送問題
3つの工場(A, B, C)から4つの倉庫(1, 2, 3, 4)に製品を輸送するコストを最小化する問題を考えます。各工場の生産能力と各倉庫の需要量、および各ルートの輸送コストは以下の通りです:
工場の生産能力:
- 工場A: 100単位
- 工場B: 150単位
- 工場C: 200単位
倉庫の需要量:
- 倉庫1: 120単位
- 倉庫2: 80単位
- 倉庫3: 130単位
- 倉庫4: 120単位
輸送コスト(1単位あたり):
倉庫1 倉庫2 倉庫3 倉庫4
工場A 10 8 6 12
工場B 8 7 9 6
工場C 11 5 7 9
この問題は以下のように定式化できます。
決定変数:
$x_{ij}$ = 工場$i$から倉庫$j$へ輸送する製品の量($i \in {A, B, C}$, $j \in {1, 2, 3, 4}$)
目的関数(コスト最小化):
$$\min z = 10x_{A1} + 8x_{A2} + 6x_{A3} + 12x_{A4} + 8x_{B1} + 7x_{B2} + 9x_{B3} + 6x_{B4} + 11x_{C1} + 5x_{C2} + 7x_{C3} + 9x_{C4}$$
制約条件:
- 工場の生産能力:
- $x_{A1} + x_{A2} + x_{A3} + x_{A4} \leq 100$
- $x_{B1} + x_{B2} + x_{B3} + x_{B4} \leq 150$
- $x_{C1} + x_{C2} + x_{C3} + x_{C4} \leq 200$
- 倉庫の需要量:
- $x_{A1} + x_{B1} + x_{C1} = 120$
- $x_{A2} + x_{B2} + x_{C2} = 80$
- $x_{A3} + x_{B3} + x_{C3} = 130$
- $x_{A4} + x_{B4} + x_{C4} = 120$
- 非負制約:
- $x_{ij} \geq 0$ for all $i, j$
最適解は以下の通りです。
- 工場Aから倉庫3へ100単位
- 工場Bから倉庫1へ120単位、倉庫4へ30単位
- 工場Cから倉庫2へ80単位、倉庫3へ30単位、倉庫4へ90単位
- 総輸送コスト:3,620
5.3. 投資ポートフォリオ最適化
金融分野では、リスクとリターンのバランスを考慮した投資ポートフォリオの最適化に線形計画法が使われます。
例:ポートフォリオ最適化
投資家が5つの資産(A, B, C, D, E)に投資を検討しているとします。各資産の期待リターンとリスク(標準偏差)は以下の通りです。
資産 期待リターン リスク
A 8% 5%
B 12% 9%
C 7% 4%
D 10% 7%
E 15% 12%
投資家は1,000万円を投資し、期待リターンを少なくとも10%にしたいと考えています。また、リスク分散のために、どの資産にも全体の40%以上は投資しないことにします。
決定変数:
$x_i$ = 資産$i$に投資する割合($i \in {A, B, C, D, E}$)
目的関数(リスク最小化):
$$\min z = 5x_A + 9x_B + 4x_C + 7x_D + 12x_E$$
制約条件:
- 投資総額:$x_A + x_B + x_C + x_D + x_E = 1$
- 期待リターン:$8x_A + 12x_B + 7x_C + 10x_D + 15x_E \geq 0.1$
- 分散制約:$x_i \leq 0.4$ for all $i$
- 非負制約:$x_i \geq 0$ for all $i$
5.4. その他の応用例
- 栄養計画:必要な栄養素を最小コストで摂取する食事計画
- スケジューリング:作業や工程の最適なスケジュール作成
- 人員配置:シフトや人材の最適な割り当て
6. 線形計画法の限界と拡張
6.1. 整数計画法
実際の問題では、変数が整数値しか取れない場合があります(例:製品の生産個数、人員配置など)。この場合、整数計画法(Integer Programming)が用いられます。代表的な解法としては分枝限定法(Branch and Bound)があります。
6.2. 非線形計画法
目的関数や制約条件が非線形(二次関数など)の場合は、非線形計画法(Nonlinear Programming)が必要になります。例えば、ポートフォリオ最適化におけるリスク最小化は二次計画問題となります。
6.3. 確率的計画法
パラメータに不確実性がある場合、確率的計画法(Stochastic Programming)を用いることができます。例えば、将来の需要や価格が不確実な場合の生産計画などに適用されます。
6.4. 双対問題と感度分析
線形計画問題には「双対問題」と呼ばれる関連問題があります。双対問題を解くことで、元の問題(主問題)の解に関する追加情報を得ることができます。
| 要素 | 主問題(Primal Problem) | 双対問題(Dual Problem) |
|---|---|---|
| 最適化の方向 | 最大化 | 最小化 |
| 目的関数 | $$\max z = \sum_{j=1}^{n} c_j x_j$$ | $$\min w = \sum_{i=1}^{m} b_i y_i$$ |
| 制約条件 | $$\sum_{j=1}^{n} a_{ij}x_j \leq b_i \quad \text{for} \; i=1,2,\ldots,m$$ | $$\sum_{i=1}^{m} a_{ij}y_i \geq c_j \quad \text{for} \; j=1,2,\ldots,n$$ |
| 変数の制約 | $$x_j \geq 0 \quad \text{for} \; j=1,2,\ldots,n$$ | $$y_i \geq 0 \quad \text{for} \; i=1,2,\ldots,m$$ |
| 変数の数 | n個の変数 $x_j$ | m個の変数 $y_i$ |
| 制約式の数 | m個の制約 | n個の制約 |
| 制約条件の右辺 | $b_i$ (リソース量) | $c_j$ (目的関数の係数) |
| 目的関数の係数 | $c_j$ (単位利益など) | $b_i$ (制約の右辺値) |
| 制約条件の係数行列 | $A = [a_{ij}]$ | $A^T = [a_{ji}]$ (転置行列) |
| 最適解の関係 | 主問題と双対問題の最適値は等しい(強双対性定理) | |
| 相補性 |
相補スラック条件:
– 主問題の変数 $x_j$ が正なら、対応する双対問題の制約は等式で成立 – 双対問題の変数 $y_i$ が正なら、対応する主問題の制約は等式で成立 |
|
| 経済的解釈 | 資源配分問題 | 資源の価格付け問題(シャドウプライス) |
注:上記の表は「標準形」での主問題と双対問題の対応を示しています。一般的には、主問題が最大化なら双対問題は最小化、主問題の「≤」制約は双対問題では「≥」制約に対応します。また、主問題の等式制約は双対問題では符号制約のない変数に対応します。
図表6: 双対問題の対応表
感度分析は、制約条件や目的関数の係数が変化したときに最適解がどのように変化するかを分析する手法です。これにより、資源の追加価値(シャドウプライス)などの情報を得ることができます。
7. 実践:線形計画問題の解き方
7.1. 問題の定式化ステップ
- 決定変数の特定:何を決定すべきか、変数として定義
- 目的関数の設定:最大化または最小化したい評価基準
- 制約条件の特定:資源の制限、技術的制約、バランス式など
- 数学モデルの構築:変数、目的関数、制約条件を数式で表現
7.2. ソフトウェアツールの紹介
線形計画問題を解くための代表的なソフトウェアツール:
- 汎用の最適化ソルバー:
- CPLEX
- Gurobi
- GLPK(GNU Linear Programming Kit)
- プログラミング言語のライブラリ:
- Python: PuLP, SciPy
- R: lpSolve
- MATLAB: linprog
- モデリング言語:
- AMPL
- GAMS
- Julia/JuMP
7.2.1. Pythonでの実装例
# PuLPを使用した製品ミックス問題の解法
from pulp import *
# 問題の定義
prob = LpProblem("製品ミックス問題", LpMaximize)
# 変数の定義
x1 = LpVariable("テーブル", 0, None) # 非負
x2 = LpVariable("椅子", 0, None) # 非負
# 目的関数
prob += 10000 * x1 + 3000 * x2, "総利益"
# 制約条件
prob += 10 * x1 + 3 * x2 <= 100, "木材制約"
prob += 8 * x1 + 2 * x2 <= 80, "労働時間制約"
# 問題を解く
prob.solve()
# 結果を表示
print("状態:", LpStatus[prob.status])
print("テーブルの製造数:", x1.value())
print("椅子の製造数:", x2.value())
print("総利益:", value(prob.objective))
7.3. 簡単な演習問題と解説
演習問題:製品ミックス問題
会社AはX製品とY製品を製造しています。X製品1個あたりの利益は300円、Y製品1個あたりの利益は400円です。製造工程は加工と組立の2つがあり、X製品1個の製造には加工に2時間、組立に1時間かかります。Y製品1個の製造には加工に1時間、組立に3時間かかります。1日の作業時間は、加工が最大16時間、組立が最大18時間です。1日の利益を最大化するためには、X製品とY製品をそれぞれ何個製造すべきでしょうか?
解答:
- 決定変数:
- $x$:X製品の製造個数
- $y$:Y製品の製造個数
- 目的関数(利益最大化): $$\max z = 300x + 400y$$
- 制約条件:
- 加工時間制約:$2x + y \leq 16$
- 組立時間制約:$x + 3y \leq 18$
- 非負制約:$x, y \geq 0$
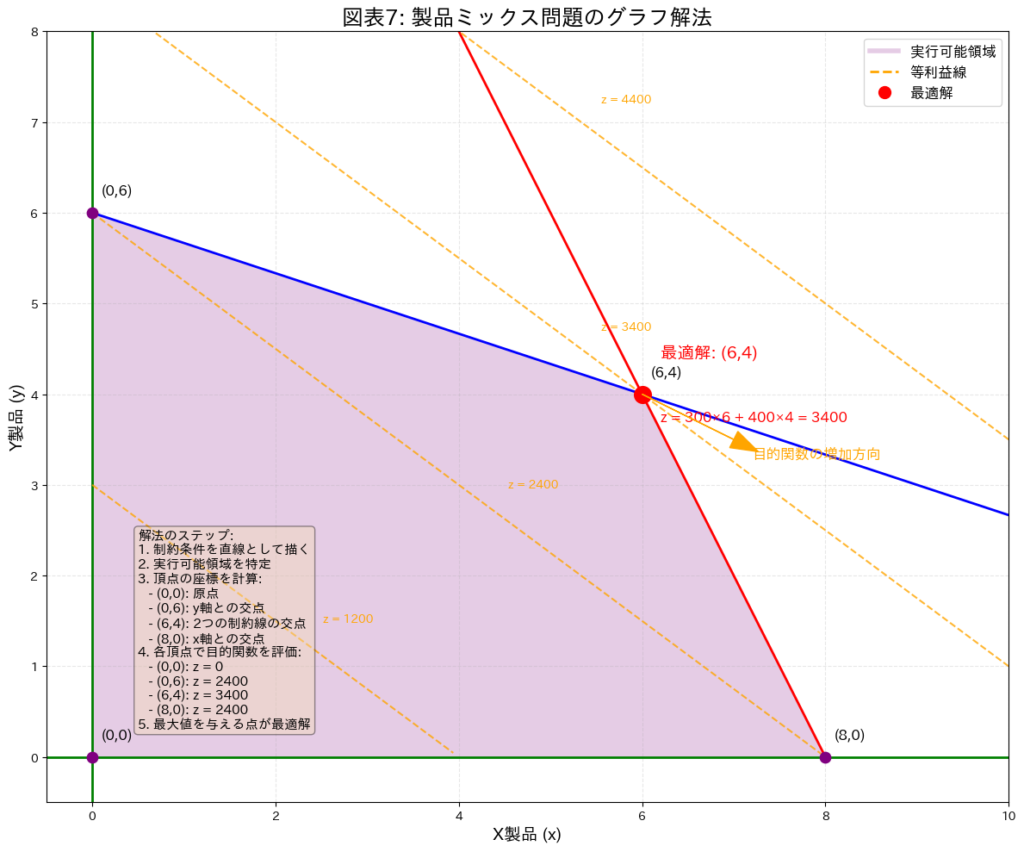
図表7: 製品ミックス問題のグラフ解法
- 図解法による解:
- 加工時間制約の直線:$2x + y = 16$
- 組立時間制約の直線:$x + 3y = 18$
- これらの直線と座標軸で囲まれた領域が実行可能領域
- 実行可能領域の頂点で目的関数を評価し、最大値を与える点を見つける
- 実行可能領域の頂点:(0, 0), (0, 6), (6, 4), (8, 0)
- 各頂点での目的関数値:
- (0, 0): $z = 0$
- (0, 6): $z = 400 \times 6 = 2400$
- (6, 4): $z = 300 \times 6 + 400 \times 4 = 3400$
- (8, 0): $z = 300 \times 8 = 2400$
- 最適解:X製品6個、Y製品4個を製造
- 最大利益:$300 \times 6 + 400 \times 4 = 3400$円
8. まとめ
線形計画法は、限られた資源の最適配分を行うための強力な数学的手法です。その特徴は以下の通りです。
- 目的関数と制約条件がすべて線形であること
- 実行可能領域は凸多面体であり、最適解はその頂点に存在すること
- シンプレックス法や内点法などの効率的な解法があること
- 多くの実用的な問題に適用可能であること
線形計画法は最適化問題の基礎となる手法であり、より複雑な問題に対しては整数計画法、非線形計画法、確率的計画法などの拡張手法が開発されています。
8.1. 線形計画法の最新研究動向
近年の線形計画法の研究と応用には、以下のような動向があります。
- 大規模問題への対応: ビッグデータ時代に対応した大規模線形計画問題を効率的に解くためのアルゴリズムの開発
- 分散最適化: 並列計算を活用した分散型アルゴリズムの研究
- 機械学習との融合: 線形計画法と機械学習を組み合わせたハイブリッドアプローチの開発
- ロバスト最適化: 不確実性を考慮した頑健な解を求めるための手法の研究
- リアルタイム最適化: オンラインでの即時解法や近似解法の開発
今後の学習のためには、以下のリソースが役立ちます:
- 線形代数と最適化理論の基礎知識
- プログラミングスキルと最適化ソルバーの使い方
- 実際の問題を数理モデルに定式化する能力
線形計画法は理論と実践の両面から学ぶことで、様々な分野での意思決定問題に応用することができます。

